In this post, I would like to talk a little bit about quantum physics and photons in terms of quantum mechanics.
(More comments and explanations will be added in a full version of the article and the last edition of the article will be published in a PDF).
Let’s start with basic measurements.
When we talk about waves – it is considered to be De Broglie waves.
Measuring of photons energy
According to quantum mechanics, you may measure photon energy by means of different methods.
One of them is offered by Planck and includes the speed of light and wavelength.
The energy of a photon is related to its frequency and–since c = λν–to its wavelength. The relation is E = hν, where h is Planck’s constant. The unit amount usually used for photons’ energy is the electron-volt (eV).
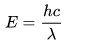
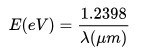
Photons energy for the 445 nm wavelength
Therefore, the photon energy at the 445 nm (0.445 μm) wavelength (the lasers we make) is approximately 2.78606 eV.
Photons energy for the 808 wavelength
Therefore, the photon energy at the 808 nm (0.808 μm) wavelength (the lasers we make) is approximately 1.534 eV.
Focusing
It is known that the minimum focus can be no less than the size of the laser wavelength.
It means that even theoretically it is impossible to get a laser spot size for a 445 nm laser smaller than 0.445 μm, which is equal to 0.000445 mm.
While modern optics allows to get a laser spot something around 0.1-0.15 mm.
This means that theoretically, the energy applied to an engraved spot can be 200 times as intensive.
CO2 laser and different wavelength
As you may see – the energy that single photons with different wavelengths may carry is different.
That is why a laser with a wavelength of 808 nm carries less energy than 445 nm wavelength laser. We can conclude that a 10 watt 445 nm laser will carry energy as a 20 watt 890 nm laser. That is why diode lasers with the 445 nm wavelength are more efficient than infrared lasers.
CO2 lasers typically emit at a wavelength of 10.6 μm, but there are other lines in the region of 9–11 μm (particularly at 9.6 μm). This means that the energy of a CO2 photon carries 20 times as little energy, something around 0.12398 eV.
And the spot size cannot be smaller than 0.01 mm.
In this case CO2 lasers bring less energy to one spot if the wattage of the emitter is the same.
It does not mean that CO2 lasers are 20 times less powerful because the density of the laser beam and the frequency of the laser momentum can be much higher than those of diode lasers with a wavelength of 445 nm or 808 nm. Also normally CO2 lasers have moer powerful emitter.
Now let’s get closer to the quantum world.
What would be the energy of a photon if its wavelength equal to the Planck’s length?
It is interesting that a single photon with a wavelength of 1.61 × 10^(−35) metres would carry 7.671 × 10^28 eV that is equal to 3413888 watt / sec of power (3.4 Gigawatt / sec). Just a single photon!
However I do not think that anyone has already registered a photon with that wavelength.
And if the wavelength of a photon would be closer to the proton radius then it would carry only 4.794 × 10^13 eV, that is equal to 2.13 x 10^(-9) watts.
Nota bene, how much less energy carries this single-photon than the one with the Planck’s wavelength.
Let’s compare photons’ momentum for different wavelength.
Measuring of photons momentum
To measure the momentum of the photon we will take another equation
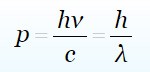
For h we use 6.62 × 10^(-34) value
Photon momentum for the 445 nm wavelength
p = 1.48 x 10^(-33) (kg × m)/s
Photon momentum for the 808 nm wavelength
p = 8.2 x 10^(-34) (kg × m)/s
Photon momentum for the 10000 nm wavelength (CO2 lasers)
p = 6.626 × 10^(-38) (kg × m)/s
What if the wavelength of
the photon changes?
It is not proven that photon wavelength can be changed, however changing the photon wavelength will require changing of the momentum or the energy of the photon it carries.
Since the photon does not seem to interact (collide) with other particles, thus, neither increase nor decrease of the momentum or energy take place, – it is quite possible that the photon has a constant wavelength during its lifetime. Still it is a big question in quantum mechanics.
However, theoretically, there is a chance that a photon can lose its momentum due to the quantum effects that occur while virtual particles appear and annihilate. There is a chance that photons can interact (collide) with them and, therefore, its wavelength can change (more likely increase). There is a theory of “tired light”. The “tired light” theory claims that the light of distant galaxies reddens because it loses energy as it passes through space.
The theory of “tired light” has a lot of weak spots for example that while losing energy – the wavelength would increase and distant galaxies would be more diffuse therefore this is not observed.
This effect is called “redshift”. Many scientists think that it happens because of the universe expansion caused by the unseen immeasurable dark energy. In my opinion, the wavelength of light can simply inflate due to the quantum effects. This could be caused by the expansion of the universe effect.
I would like to present another calculation that might be interesting as well
Some calculations and some conclusions I want to present
eV in 1 watt x sec 6.24 x 10^18
eV in 10 watt x sec 6.24 x 10^19
eV for 445 nm photon 2.78
The number of photons in a 10 watt laser 445 nm 2.24 x 10^19
eV for 808 nm photon 1.53
The number of photons in a 10 watt laser 808 nm 4.06 x 10^19
eV for 10000 nm (CO2 laser) photon 0.12
The number of photons in a 10 watt laser 10000 nm 5.03 x 10^20
It is notable that a CO2 laser needs 20 times as many photons to perform the same work.
The emitting spot for a 10 watt 445 nm laser, uM 100
The emitting spot for a 10 watt 808 nm laser, uM 200
(we take these parameters as is from the laser diode data sheets)
The number of photons that are emitted in 1 uM space for 445 nm laser 2.24 x 10^17
The number of photons that are emitted in 1 uM space for 808 nm laser 2.03 x 10^17
This data literally says, the more power you want to get – the bigger should be the emitting size, and as you can see the amount of the photons created for a 445 nm laser and a 808 nm laser is relatively the same since 445 nm laser has smaller emitting spot comparing to 808 nm laser.
Here I want to talk about black holes and ability to create a laser powerful enough to create a black hole
Deeper philosophical conclusions
The Sun mass, kg 1.98 x 10^30
A minimum black hole mass, kg 1.98 x 10^31
The energy of a black hole, joules 1.78 x 10^48
1 joule in eV 6.24 x 10^18
A photon with a wavelength equal to Planck’s carries, eV 7.67 x 10^28
The energy of a black hole, eV 1.11 x 10^67
A number of photons to create a black hole with the Planck’s wavelength 1.45 x 10^38
A number of photons to create a black hole with the 1 nm wavelength 9.00 x 10^63
A number of photons to create a black hole with the 445 nm wavelength 4.00 x 10^66
These numbers are hard to imagine and understand. However, we are going to estimate the laser parameters needed to form a black hole.
The laser power to create the energy of a black hole with 1 Hz Frequency, W 1.78 x 10^48
The laser power to create the energy of a black hole with 1 GHz Frequency, W 1.78 x 10^39
The laser power to create the energy of a black hole with 1 GHz Frequency, GW 1.78 x 10^30
The laser power for 445 nm to create the energy of a black hole, for 1 GHz Frequency. GW 6.41 x 10^29
The laser power for 0.0045 nm (Gamma-ray) to create the energy of a black hole, for 1 GHz Frequency. GW 6.48 x 10^24
The emitting spot size of a 10 watt 445 nm laser to generate the mentioned above energy should be uM 1.78 x 10^49
or Km 1.78 x 10^37
A 10 watt laser should have a frequency of 1GHz, Km 1.78 x 10^28
The size of the Milky Way, Km 1 x 10^18
The size of the Universe, Km 8.8 x 10^23
Thus, to create a black hole with a 10 watt laser the length of the emitter aimed at one spot of space should be 1 х10^28, while the Universe size is Km 8.8 x 10^23 (of course if you set them serial).
However, there might be another method of calculations:
Let take Schwarzschilder’s equation.
The Schwarzschild radius for the black hole, Km 29.49
The volume of a black hole, Km^3 107 440.20
The volume of a black hole, nm^3 1.07 x 10^32
The energy density of a black hole in 1 nm^3, eV 1.038 x 10^35
Watt of energy in 1 nm^3 for 1 Hz in a black hole 1.66 x 10^16
Watt of energy in 1 nm^3 for 1 GHz in a black hole 16 635 189.63
In other words, to create a black hole you would need to aim a 16 Megawatt 1GHz laser at a spot of 1.07 x 10^32.
However, if the black hole is consistent it means that a 16MW and a 1 GHz lasers will be able to create a mini black hole in a nm^3 space!
It is possible since The photon as a gauge boson therefore the number of photons in one space can be unlimited.
Physicists continue to hypothesize grand unified theories that connect these four gauge bosons with the eight gluon gauge bosons of quantum chromodynamics; however, key predictions of these theories, such as proton decay, have not been observed experimentally.
What I am going to do next
In my further research, I plan to explore and talk more about virtual particles that appear in the Space and if these particles can interact (collide) with photons and somehow change its speed (unlikely), energy / wavelength / momentum.
If there is any way that photons can gain/lose energy?
Another question if an electro-magnetic field can change the route of a photon.
We can build a model an electro-magnetic field with Kilovolts energies and see if it will bend a laser beam.
Something like a Tesla coil.
Another thing that I’m going to collect more data concerning parameters of CO2, fiber and diode lasers, such as: their frequencies, emitting area sizes, densities of the emitting light, laser temperature dependence on a wavelength, to make better comparisons.
For example it is interesting to see if diode / CO2 / fiber lasers will have different wavelength if we decrease a temperature to -50-100C. We would need liquid nitrogen or oxygen for this experiment.
We also plan to make some experiments with Bose-Einstein condensate and diode lasers.
It was proven that the speed of light may decrease in a Bose-Einstein condensate. It is still not obvious how to get a gas with a temperature close to absolute 0 (K) but maybe with a higher temperature Bose-Einstein condensate can be observed.
(We plan to add more research to this topic…)
Researchers, quantum physicists are welcome to add comments, make posts and share ideas.
