Waist of single-mode laser radiation – determining the depth of focus.

Assignment:

We need to focus a single-mode beam with a given waist length L_w.

A single-mode beam is Gaussian, for which there is an expression:

where: ω(z) is the beam radius (field strength level 1/е²), ω₀ is the same but in the waist (at z=0), λ is the radiation wavelength.

If we switch to transverse dimensions not by field strength but by intensity and use the diamter instead of the radius, then:

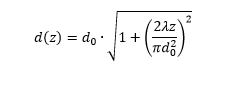
where: d is the diameter (by 1/е² intensity level).

By the waist length, we usually understand the length of a segment near the waist where the beam diameter does not exceed twice the diameter in the waist d₀. Then for the waist length L_w we have:

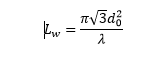
Using it, we get the beam diameter in the waist length d₀ :

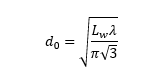
At L_w = 10-15 mm, d₀ = (44-54) µm.

Usually, the beam exiting the fiber should be collimated first before focusing. In this case the focused beam diameter equals :

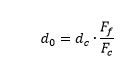
where: d_c is the central fiber core, F_c and F_f are focus lengths of the collimating and focusing lenses.

Since the numerical aperture of single-mode fibers is usually small, and the numerical aperture of focused radiation is even smaller, ordinary spherical lenses will do for collimating and focusing. The lens diameter must be equal to or more than a certain value:

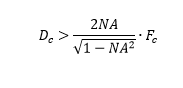
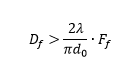
where: D_c and D_f are diameters of the collimating and the focusing lenses, correspondingly,

NA is a numering aperture of the fiber.